Introduction
Given the increasing use of the wireless radio spectrum, new spectrum sharing techniques for radar and communication are in high demand. Dynamic spectrum for sharing between radar and communications has been prominently featured in the 3.55 to 3.65 GHz and 5 GHz radar bands. We recently proposed and described the construction of a dynamic spectral mask for the radar transmission based on the locations and maximum acceptable interference power levels of nearby communication handset receivers [1]. In the present paper, we use the dynamically determined spectral mask with an alternating-projections waveform optimization to optimize the waveform for ambiguity function (AF) and spectral mask compliance [2], [3].
This method will be useful for implementing cognitive radar, defined as a radar that can sense and respond to its environment [4] and is aided by knowledge that it gains from its environment [5]. Haykin discusses adjusting radar transmitter power in order to not exceed the maximum interference temperature of a receiver [6] and altering the radar transmitter waveform based on multiple criteria [7]. Mahmoud describes spectrum shaping for communications transmission based on a flexible spectral mask and licensed users in a band [8]. Srinivasa suggests applying a spectral mask to secondary users based on interference to primary users [9].
Ambiguity-Function Waveform Optimization Using a Dynamic Spectral Mask
Radar
transmission can be dynamically controlled based on the real-time
positions of surrounding wireless communication spectrum users and their
maximum acceptable interference power levels [1].
The Friis equation can be used to find the maximum power that can be
transmitted by the radar at the handset's frequency without interfering,
based on acceptable receiver power:
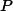


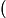
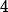
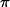
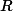
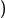

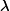

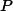


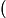
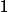
![]()
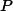

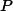

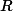
Maximum acceptable interference power levels and positions of the wireless communication handsets must be available to the radar, perhaps via a wireless network. This is reasonable given parallel developments in wireless ad-hoc networks for cognitive radio and radar operations.
Optimization
of the radar waveform to meet ambiguity function requirements and
spectral criteria is detailed in a recent conference paper [10] and summarized briefly here. Woodward's ambiguity function is the output of the radar's correlation operation for a waveform 
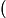
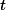
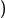

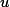
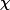



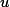
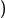

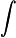

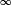
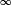

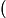
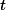
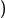


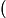
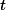




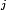




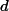
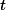

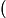
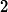
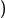
![]()
An alternating projections approach is used to project the AF of the initial waveform onto the ambiguity minimization function 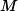


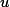

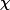



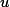


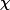


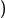


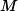
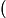


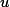
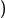


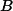
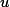
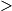
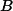

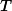



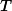
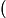
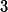
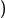
![]()
The minimization
function is used to drive the AF to be minimized at certain
range/Doppler combinations of interest in the ambiguity plane (such as
range-Doppler combinations of potentially interfering targets).
Projection of the AF 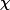

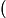


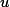
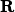
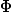

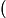


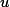
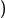

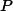
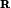
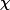

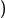


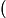


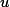
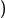
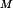
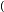







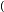






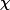

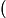


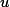
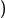

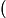


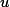
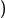
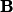


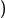
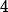
![]()
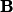
The waveform must also be projected onto the set of waveforms with pulse duration 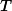
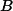
Measurement Results
At the operating frequency of 3.3 GHz, a vector signal generator was used for waveform generation and an oscilloscope was used to measure the waveform, controlled by MATLAB, which was used for scenario simulations. A scenario was constructed consisting of a radar transmitter and numerous wireless handsets communicating with two base stations. The handsets are assigned random positions and velocities within the defined spatial range, and are not allowed to leave the boundaries. The receiver sensitivity of each handset is assumed to increase with increasing distance from its base station, as the handset must discern lower-power signals. As sensitivity increases, it is assumed that the maximum acceptable interference power decreases. Thus, each handset's position with respect to both its base station and the radar transmitter will affect the dynamic spectral mask.
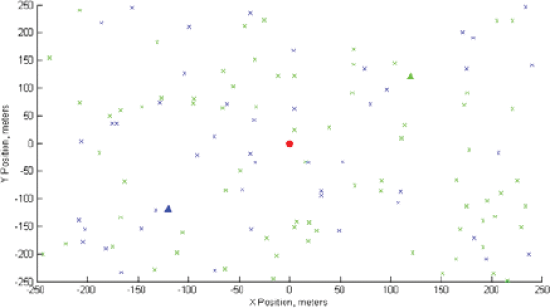
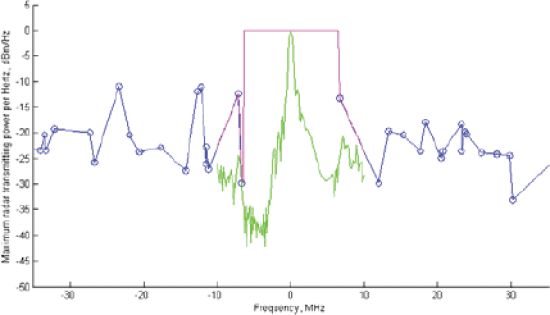
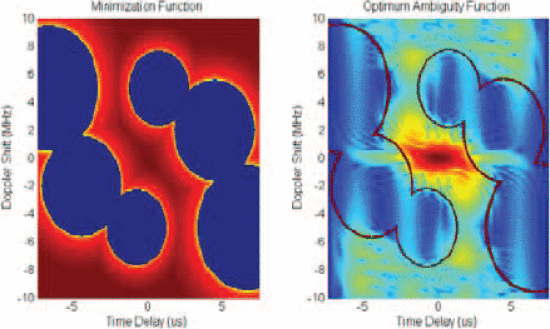
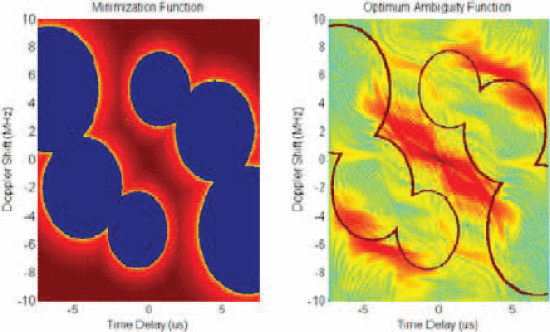
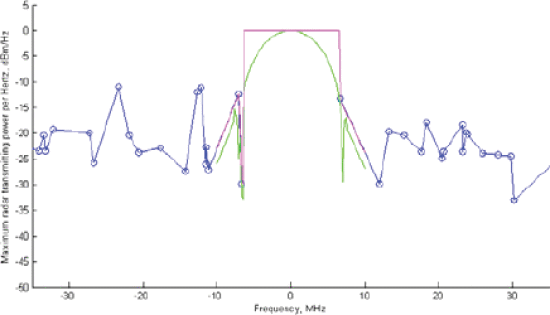
Figure 1 shows a position scenario snapshot with several moving communication handsets, corresponding to two different communication base stations, moving near a radar transmitter. Figure 2 shows the spectral mask for the position scenario described by Fig. 1, and Figure 3 shows the AF minimization template, as well as the optimized AF after 25 iterations. No PAPR constraint is imposed in the optimization shown in Figures 2 and 3. Figure 3 shows that the AF is very small in the range/Doppler regions indicated for minimization.
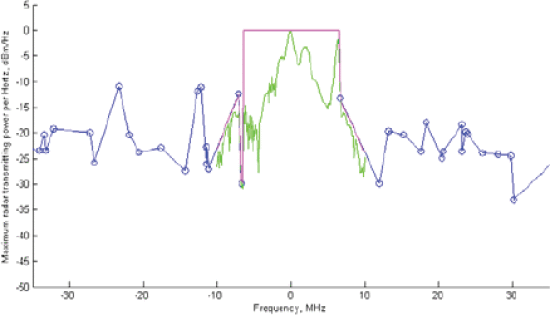
When a PAPR requirement is imposed on Fig. 1 scenario, a wider-bandwidth waveform results (Fig. 4). The dynamic spectral mask notches the transmitted spectrum. Figure 5 shows that the PAPR constraint causes ambiguity to leak into the minimization regions at certain range-Doppler combinations.
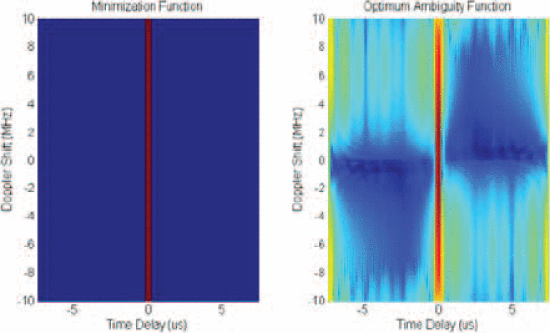
Figure 6 shows the waveform resulting from the minimization template of Fig. 7, using the Fig. 1 scenario of Fig. 1 with no PAPR requirement. This template is designed to maximize range resolution, and produces a wide-bandwidth waveform (Fig. 6) that is very close to spectral mask limitations. The AF shows good compliance with the minimization template.
Snapshot of position scenario with radar transmitter, communication handsets, and communication base stations after 25 iterations
Dynamic spectral mask (red and blue) and optimized waveform (green) derived from the fig. 1 position scenario after 25 iterations, with no PAPR constraint. Blue dots represent allowable radar transmit power density values mapped from the handsets' maximum interference power density values.
Ambiguity function minimization template (left) and optimized simulated ambiguity function (right) after 25 iterations
Conclusions
A dynamic radar waveform optimization has been demonstrated, based on a real-time spectral mask generated from the changing positions of surrounding communication handsets and including ambiguity function minimization objectives, spectral mask constraints, and PAPR requirements. This optimization is expected to be useful in cognitive and adaptive radar optimization to meet spectral requirements dictated by coexistence with wireless communications.
Dynamic spectral mask (red and blue) and optimized waveform (green) derived from the fig. 1 position scenario after 25 iterations, with maximum PAPR of 2 dB
Ambiguity function minimization template (left) and optimized simulated ambiguity function (right) for the fig. 1 position scenario and maximum PAPR of 2 dB after 25 iterations
Dynamic spectral mask (red and blue) and optimized waveform (green) derived from the fig. 1 position scenario after 25 iterations
Ambiguity function minimization template (left) and optimized simulated ambiguity function (right) after 15 iterations of the alternating projections optimization.
ACKNOWLEDGMENT
This work has been funded by the National Science Foundation (Grant No. ECCS-1343316).
Keywords
- IEEE Keywords
- Author Keywords